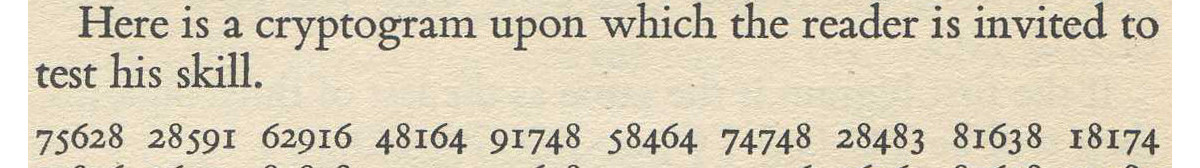Back in 1939, Alexander d’Agapeyeff wrote a small book called “Codes and Ciphers” on cryptography and its history. However, he wasn’t actually a cryptographer himself: rather, he had previously written a similar book on cartography for the same publisher, and seems to have been asked to tackle cryptography.
On the very last page of the text (p.144), d’Agapeyeff presented a challenge cipher to the reader, saying “Here is a cryptogram upon which the reader is invited to test his skill.”
75628 28591 62916 48164 91748 58464 74748 28483 81638 18174
74826 26475 83828 49175 74658 37575 75936 36565 81638 17585
75756 46282 92857 46382 75748 38165 81848 56485 64858 56382
72628 36281 81728 16463 75828 16483 63828 58163 63630 47481
91918 46385 84656 48565 62946 26285 91859 17491 72756 46575
71658 36264 74818 28462 82649 18193 65626 48484 91838 57491
81657 27483 83858 28364 62726 26562 83759 27263 82827 27283
82858 47582 81837 28462 82837 58164 75748 58162 92000
This cryptogram, now known as “the d’Agapeyeff Cipher”, has not been broken in over 70 years.
Brief analysis
Note that the digits in adjacent columns are formed alternately from 67890 and 12345 characters respectively: which strongly implies that what we are looking at is a grid cipher, where each pair of numbers gives a position in a 5×5 grid. If so, then we can discard the spaces between the blocks of numbers and instead rearrange them as pairs.
75 62 82 85 91 62 91 64 81 64 91 74 85 84 64 74 74 82 84 83 81 63 81 81 74 74 82 62 64 75 83 82 84 91 75 74 65 83 75 75 75 93 63 65 65 81 63 81 75 85 75 75 64 62 82 92 85 74 63 82 75 74 83 81 65 81 84 85 64 85 64 85 85 63 82 72 62 83 62 81 81 72 81 64 63 75 82 81 64 83 63 82 85 81 63 63 63 04 74 81 91 91 84 63 85 84 65 64 85 65 62 94 62 62 85 91 85 91 74 91 72 75 64 65 75 71 65 83 62 64 74 81 82 84 62 82 64 91 81 93 65 62 64 84 84 91 83 85 74 91 81 65 72 74 83 83 85 82 83 64 62 72 62 65 62 83 75 92 72 63 82 82 72 72 83 82 85 84 75 82 81 83 72 84 62 82 83 75 81 64 75 74 85 81 62 92 00 0[0]
The first hint that the order of these might have been scrambled (‘transposed’) comes from the two sets of tripled letters: 75 75 75 and 63 63 63. Five centuries ago, even Cicco Simonetta and his Milanese cipher clerks knew that tripled letters are very rare (the only one in Latin is “uvula“, ‘little egg’). The second hint that this is a transposition cipher is the total number of characters (apart from the “00” filler at the end): 14×14. If we discard the filler & rearrange the grid we get:-
75 62 82 85 91 62 91 64 81 64 91 74 85 84
64 74 74 82 84 83 81 63 81 81 74 74 82 62
64 75 83 82 84 91 75 74 65 83 75 75 75 93
63 65 65 81 63 81 75 85 75 75 64 62 82 92
85 74 63 82 75 74 83 81 65 81 84 85 64 85
64 85 85 63 82 72 62 83 62 81 81 72 81 64
63 75 82 81 64 83 63 82 85 81 63 63 63 04
74 81 91 91 84 63 85 84 65 64 85 65 62 94
62 62 85 91 85 91 74 91 72 75 64 65 75 71
65 83 62 64 74 81 82 84 62 82 64 91 81 93
65 62 64 84 84 91 83 85 74 91 81 65 72 74
83 83 85 82 83 64 62 72 62 65 62 83 75 92
72 63 82 82 72 72 83 82 85 84 75 82 81 83
72 84 62 82 83 75 81 64 75 74 85 81 62 92
This is very probably the starting point for the real cryptography (though the presence of tripled characters in the columns implies that it probably isn’t a simple “matrix-like” diagonal transposition. Essentially, it seems that we now have to solve a 14×14 transposition cipher and a 5×5 substitution cipher simultaneously, over a relatively small cryptogram – an immense number of combinations to explore.
But can we solve it?